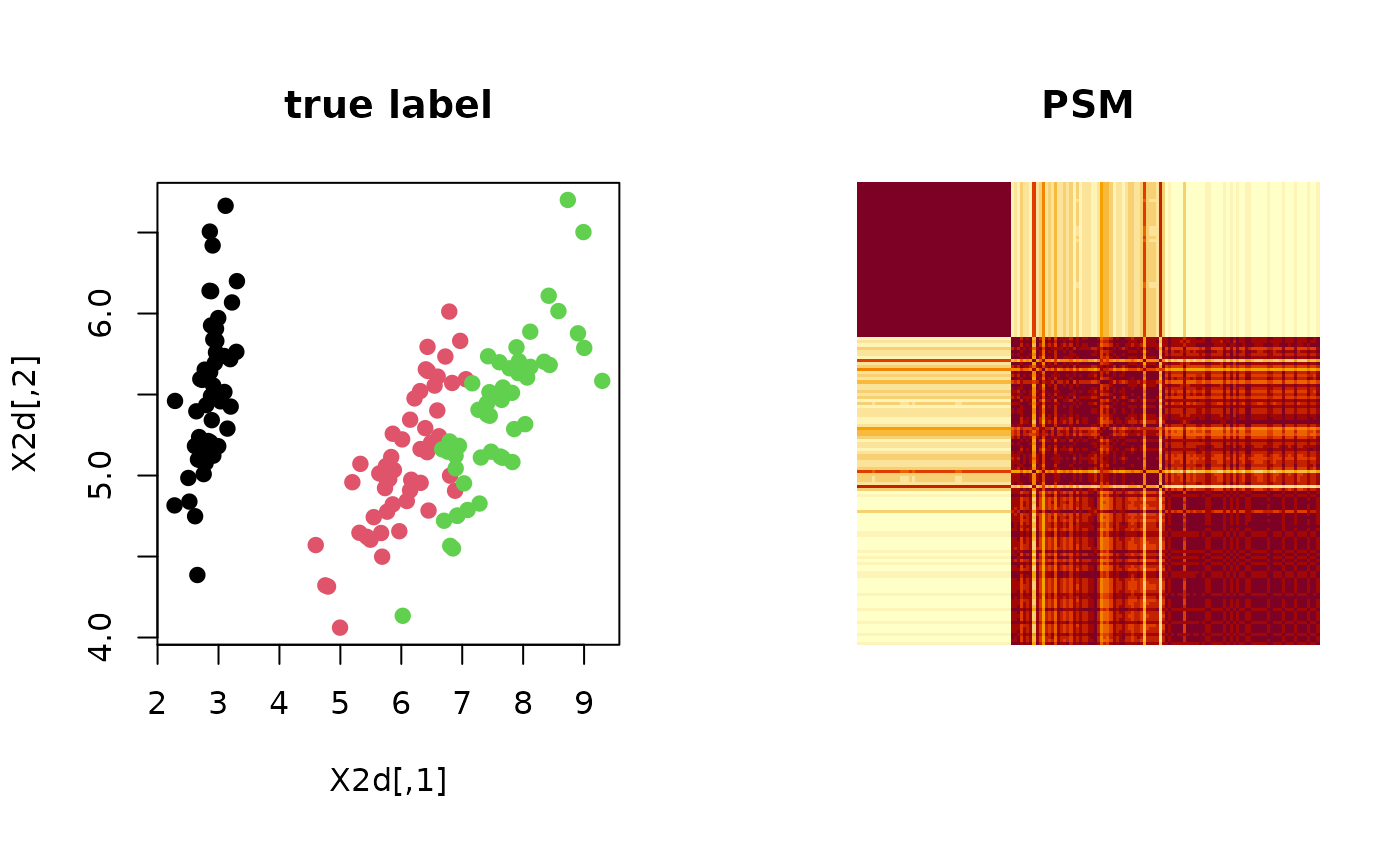Let clustering be a label from data of \(N\) observations and suppose
we are given \(M\) such labels. Posterior similarity matrix, as its name suggests,
computes posterior probability for a pair of observations to belong to the same cluster, i.e.,
$$P_{ij} = P(\textrm{label}(X_i) = \textrm{label}(X_j))$$
under the scenario where multiple clusterings are samples drawn from a posterior distribution within
the Bayesian framework. However, it can also be used for non-Bayesian settings as
psm is a measure of uncertainty embedded in any algorithms with non-deterministic components.
psm(partitions)
Arguments
| partitions | partitions can be provided in either (1) an \((M\times N)\) matrix where each row is a clustering for \(N\) objects, or (2) a length-\(M\) list of length-\(N\) clustering labels. |
|---|
Value
an \((N\times N)\) matrix, whose elements \((i,j)\) are posterior probability for an observation \(i\) and \(j\) belong to the same cluster.
See also
Examples
# ------------------------------------------------------------- # PSM with 'iris' dataset + k-means++ # ------------------------------------------------------------- ## PREPARE WITH SUBSET OF DATA data(iris) X = as.matrix(iris[,1:4]) lab = as.integer(as.factor(iris[,5])) ## EMBEDDING WITH PCA X2d = Rdimtools::do.pca(X, ndim=2)$Y ## RUN K-MEANS++ 100 TIMES partitions = list() for (i in 1:100){ partitions[[i]] = kmeanspp(X)$cluster } ## COMPUTE PSM iris.psm = psm(partitions) ## VISUALIZATION opar <- par(no.readonly=TRUE) par(mfrow=c(1,2), pty="s") plot(X2d, col=lab, pch=19, main="true label") image(iris.psm[,150:1], axes=FALSE, main="PSM")