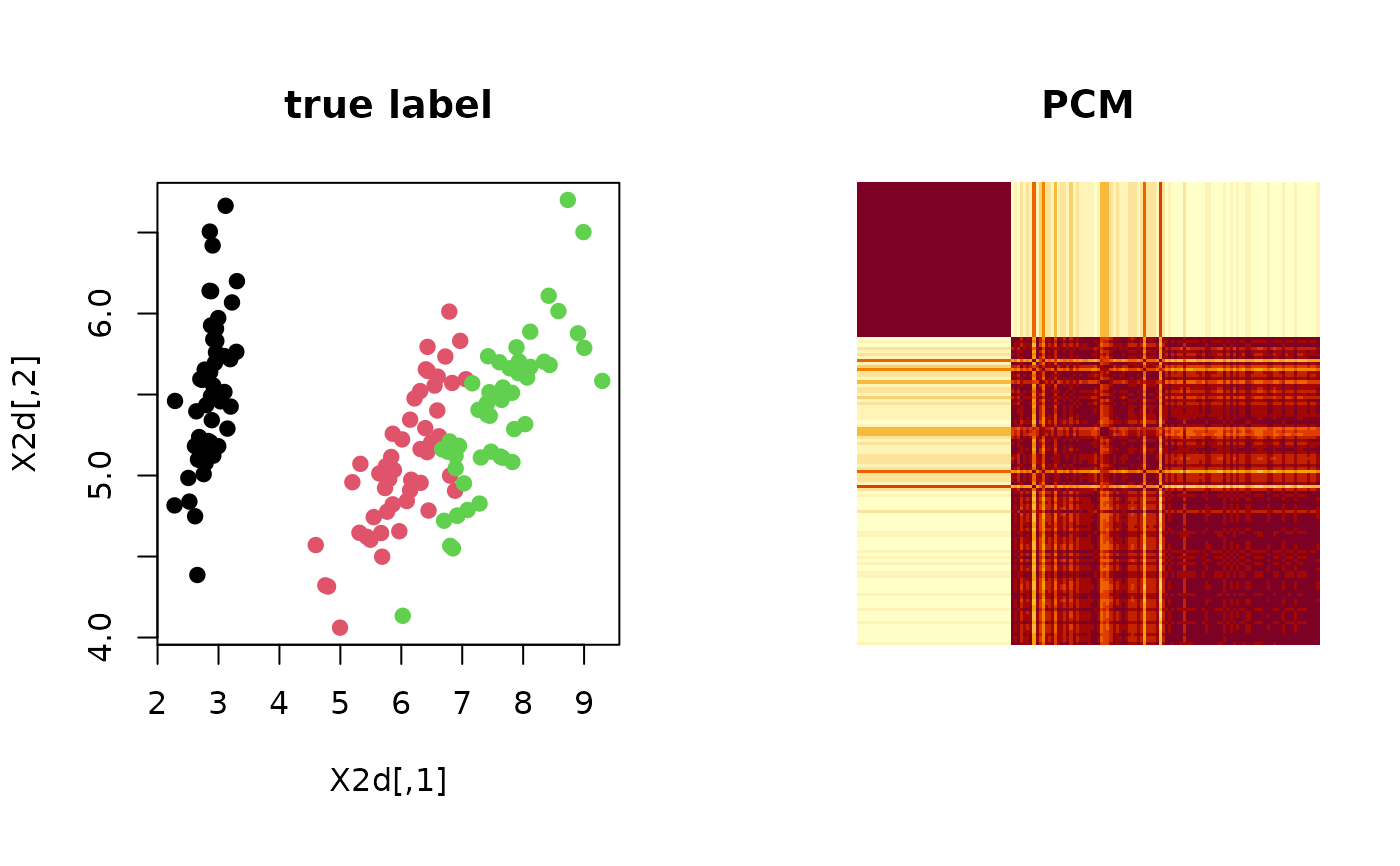Compute Pairwise Co-occurrence Matrix

Let clustering be a label from data of \(N\) observations and suppose we are given \(M\) such labels. Co-occurrent matrix counts the number of events where two observations \(X_i\) and \(X_j\) belong to the same category/class. PCM serves as a measure of uncertainty embedded in any algorithms with non-deterministic components.

pcm(partitions)

Arguments

partitions	partitions can be provided in either (1) an \((M\times N)\) matrix where each row is a clustering for \(N\) objects, or (2) a length-\(M\) list of length-\(N\) clustering labels.

Value

an \((N\times N)\) matrix, whose elements \((i,j)\) are counts for how many times observations \(i\) and \(j\) belong to the same cluster, ranging from \(0\) to \(M\).

See also

psm

Examples

# -------------------------------------------------------------
#               PSM with 'iris' dataset + k-means++
# -------------------------------------------------------------
## PREPARE WITH SUBSET OF DATA
data(iris)
X     = as.matrix(iris[,1:4])
lab   = as.integer(as.factor(iris[,5]))

## EMBEDDING WITH PCA
X2d = Rdimtools::do.pca(X, ndim=2)$Y

## RUN K-MEANS++ 100 TIMES
partitions = list()
for (i in 1:100){
  partitions[[i]] = kmeanspp(X)$cluster
}

## COMPUTE PCM
iris.pcm = pcm(partitions)

## VISUALIZATION
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2), pty="s")
plot(X2d, col=lab, pch=19, main="true label")
image(iris.pcm[,150:1], axes=FALSE, main="PCM")
par(opar)