Robust PCA (RPCA) is not like other methods in this package as finding explicit low-dimensional embedding with reduced number of columns. Rather, it is more of a decomposition method of data matrix \(X\), possibly noisy, into low-rank and sparse matrices by solving the following, $$\textrm{minimize}\quad \|L\|_* + \lambda \|S\|_1 \quad{s.t.} L+S=X$$ where \(L\) is a low-rank matrix, \(S\) is a sparse matrix and \(\|\cdot\|_*\) denotes nuclear norm, i.e., sum of singular values. Therefore, it should be considered as preprocessing procedure of denoising. Note that after RPCA is applied, \(L\) should be used as kind of a new data matrix for any manifold learning scheme to be applied.
Arguments
- X
an \((n\times p)\) matrix or whose rows are observations and columns represent independent variables.
- mu
an augmented Lagrangian parameter
- lambda
parameter for the sparsity term \(\|S\|_1\). Default value is given accordingly to the referred paper.
- ...
extra parameters including
- maxiter
maximum number of iterations (default: 100).
- abstol
absolute tolerance stopping criterion (default: 1e-8).
Value
a named list containing
- L
an \((n\times p)\) low-rank matrix.
- S
an \((n\times p)\) sparse matrix.
- algorithm
name of the algorithm.
References
Candès EJ, Li X, Ma Y, Wright J (2011). “Robust Principal Component Analysis?” Journal of the ACM, 58(3), 1--37.
Examples
# \donttest{
## load iris data and add some noise
data(iris, package="Rdimtools")
set.seed(100)
subid = sample(1:150,50)
noise = 0.2
X = as.matrix(iris[subid,1:4])
X = X + matrix(noise*rnorm(length(X)), nrow=nrow(X))
lab = as.factor(iris[subid,5])
## try different regularization parameters
rpca1 = do.rpca(X, lambda=0.1)
rpca2 = do.rpca(X, lambda=1)
rpca3 = do.rpca(X, lambda=10)
## apply identical PCA methods
Y1 = do.pca(rpca1$L, ndim=2)$Y
Y2 = do.pca(rpca2$L, ndim=2)$Y
Y3 = do.pca(rpca3$L, ndim=2)$Y
## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
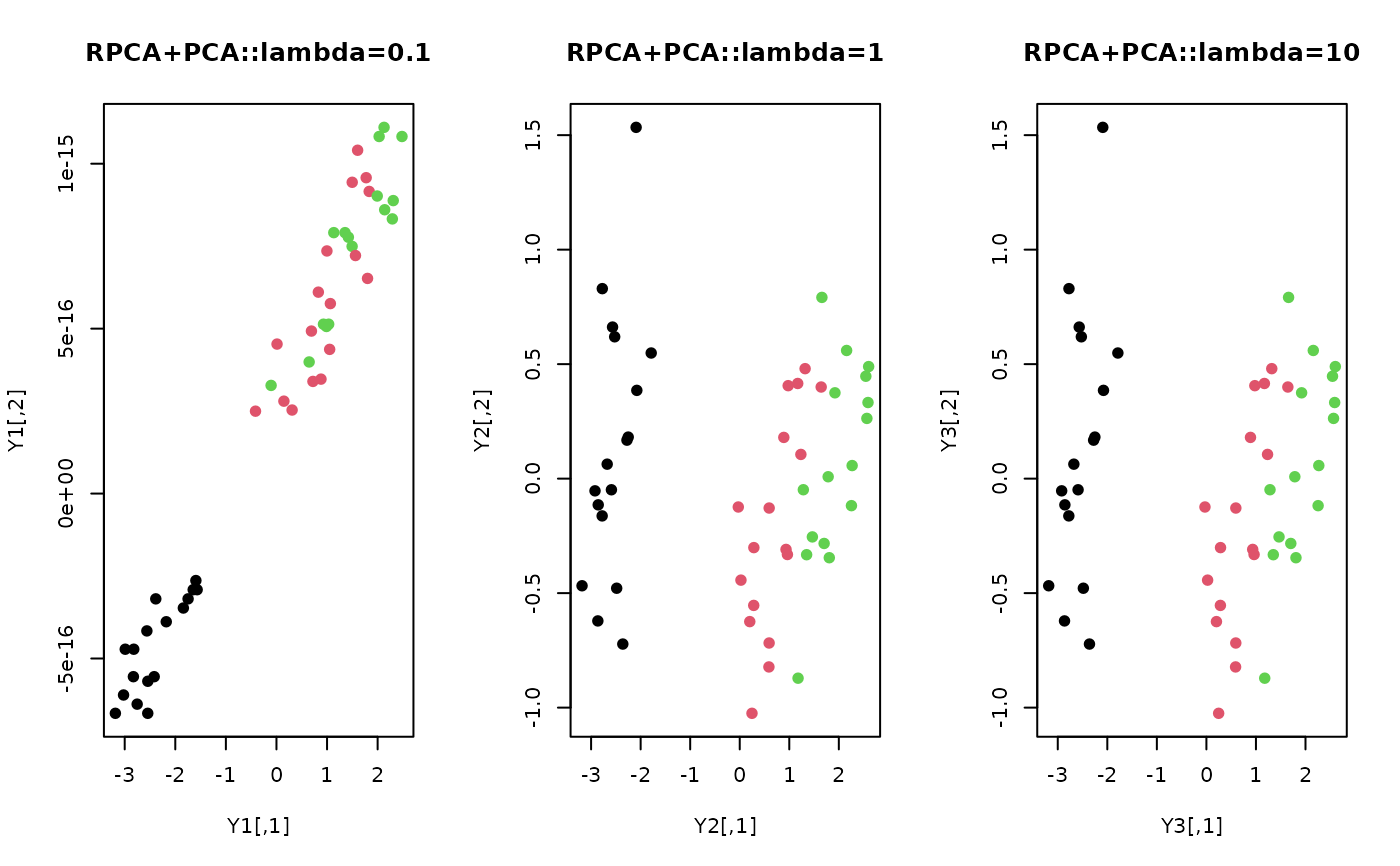
plot(Y1, pch=19, col=lab, main="RPCA+PCA::lambda=0.1")
plot(Y2, pch=19, col=lab, main="RPCA+PCA::lambda=1")
plot(Y3, pch=19, col=lab, main="RPCA+PCA::lambda=10")
 par(opar)
# }
par(opar)
# }