Principal Component Analysis

do.pca performs a classical principal component analysis (Pearson 1901) using RcppArmadillo package for faster and efficient computation.

do.pca(X, ndim = 2, ...)

Arguments

X

an \((n\times p)\) matrix whose rows are observations and columns represent independent variables.

ndim

an integer-valued target dimension.

...

extra parameters including

cor

mode of eigendecomposition. FALSE for decomposing covariance matrix (default), and TRUE for correlation matrix.

preprocess

an additional option for preprocessing the data. Default is "center". See also aux.preprocess for more details.

Value

a named Rdimtools S3 object containing

Y

an \((n\times ndim)\) matrix whose rows are embedded observations.

vars

a vector containing variances of projected data onto principal components.

projection

a \((p\times ndim)\) whose columns are basis for projection.

trfinfo

a list containing information for out-of-sample prediction.

algorithm

name of the algorithm.

References

Pearson K (1901). “LIII. On Lines and Planes of Closest Fit to Systems of Points in Space.” Philosophical Magazine Series 6, 2(11), 559--572.

Author

Kisung You

Examples

# \donttest{
## use iris data
data(iris)
set.seed(100)
subid = sample(1:150,50)
X     = as.matrix(iris[subid,1:4])
lab   = as.factor(iris[subid,5])

## try covariance & correlation decomposition
out1 <- do.pca(X, ndim=2, cor=FALSE)
out2 <- do.pca(X, ndim=2, cor=TRUE)

## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2))
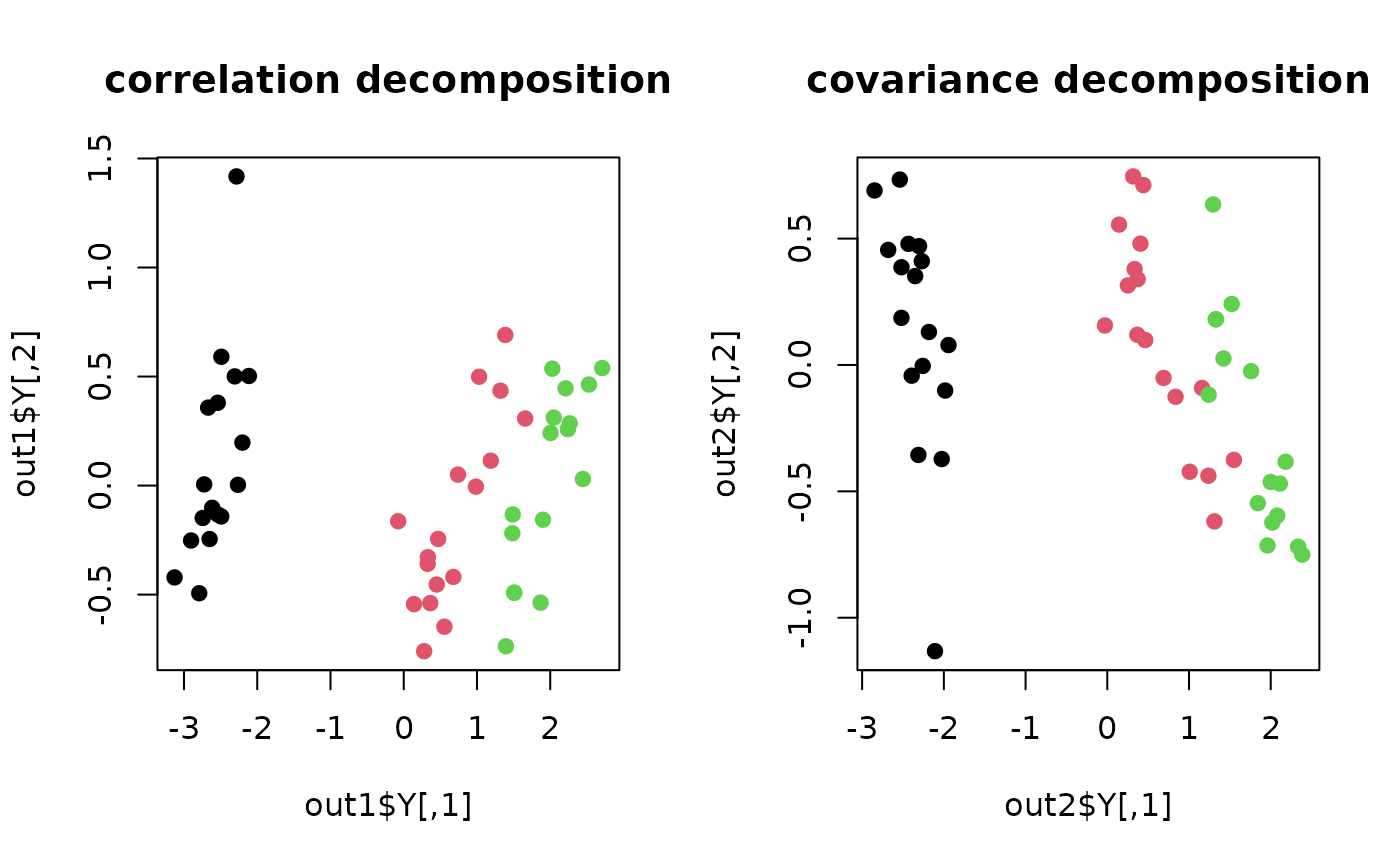
plot(out1$Y, col=lab, pch=19, main="correlation decomposition")
plot(out2$Y, col=lab, pch=19, main="covariance decomposition")

par(opar)
# }