Sparse PCA (do.spca) is a variant of PCA in that each loading - or, principal
component - should be sparse. Instead of using generic optimization package,
we opt for formulating a problem as semidefinite relaxation and utilizing ADMM.
do.spca(X, ndim = 2, mu = 1, rho = 1, ...)Arguments
- X
an \((n\times p)\) matrix whose rows are observations and columns represent independent variables.
- ndim
an integer-valued target dimension.
- mu
an augmented Lagrangian parameter.
- rho
a regularization parameter for sparsity.
- ...
extra parameters including
- maxiter
maximum number of iterations (default: 100).
- abstol
absolute tolerance stopping criterion (default: 1e-8).
- reltol
relative tolerance stopping criterion (default: 1e-4).
Value
a named Rdimtools S3 object containing
- Y
an \((n\times ndim)\) matrix whose rows are embedded observations.
- projection
a \((p\times ndim)\) whose columns are basis for projection.
- algorithm
name of the algorithm.
References
Zou H, Hastie T, Tibshirani R (2006). “Sparse Principal Component Analysis.” Journal of Computational and Graphical Statistics, 15(2), 265--286.
d'Aspremont A, El Ghaoui L, Jordan MI, Lanckriet GRG (2007). “A Direct Formulation for Sparse PCA Using Semidefinite Programming.” SIAM Review, 49(3), 434--448.
Ma S (2013). “Alternating Direction Method of Multipliers for Sparse Principal Component Analysis.” Journal of the Operations Research Society of China, 1(2), 253--274.
See also
Examples
# \donttest{
## use iris data
data(iris, package="Rdimtools")
set.seed(100)
subid = sample(1:150,50)
X = as.matrix(iris[subid,1:4])
lab = as.factor(iris[subid,5])
## try different regularization parameters for sparsity
out1 <- do.spca(X,ndim=2,rho=0.01)
out2 <- do.spca(X,ndim=2,rho=1)
out3 <- do.spca(X,ndim=2,rho=100)
## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
plot(out1$Y, col=lab, pch=19, main="SPCA::rho=0.01")
plot(out2$Y, col=lab, pch=19, main="SPCA::rho=1")
plot(out3$Y, col=lab, pch=19, main="SPCA::rho=100")
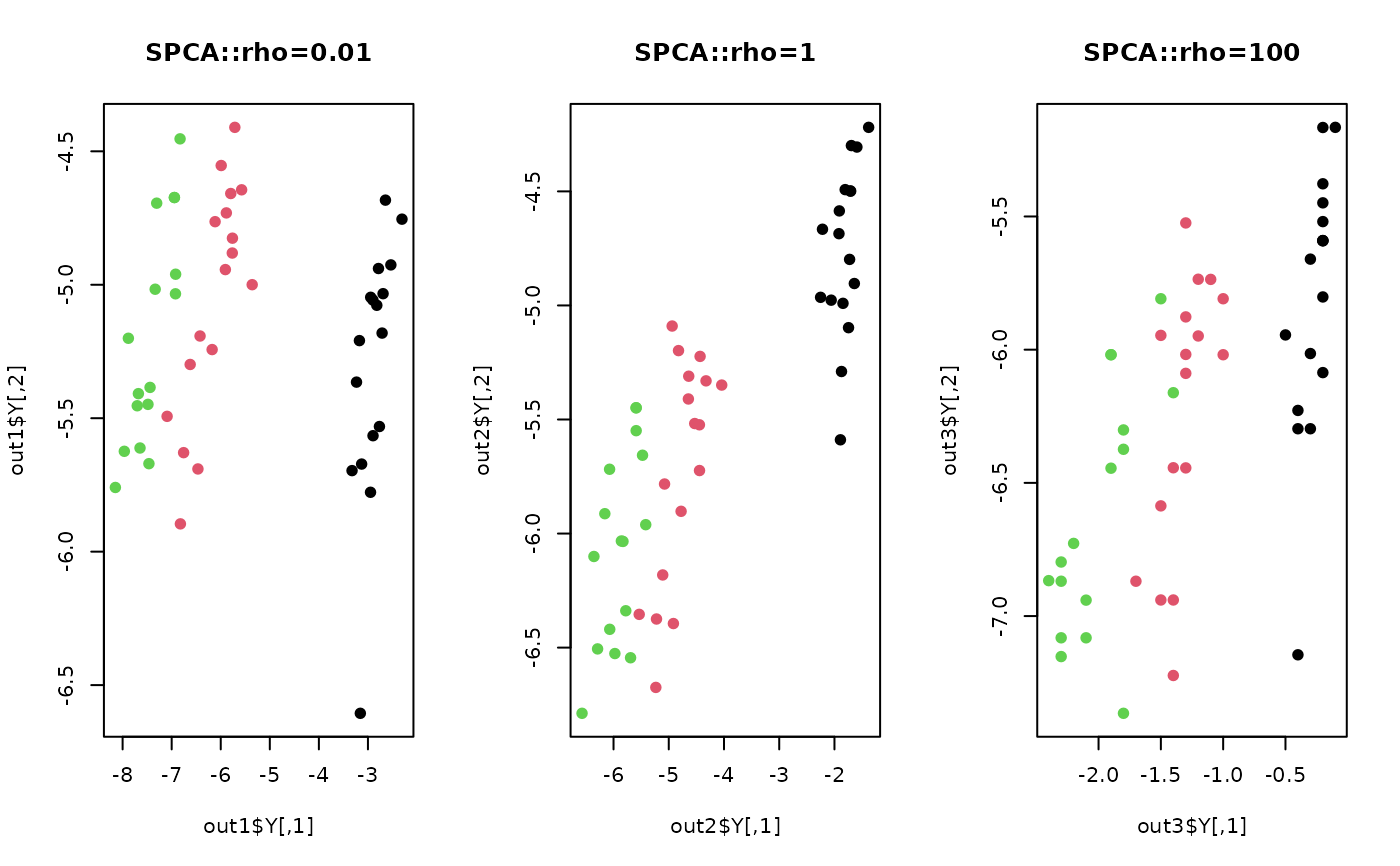 par(opar)
# }
par(opar)
# }