Barycenter of Histograms

Given multiple histograms represented as "histogram" S3 objects, compute their 2-Wasserstein barycenter using the exact 1D quantile characterization. All input histograms must have identical breaks.

Usage

histbary(hists, weights = NULL, L = 2000L)

Arguments

hists

a length-\(N\) list of histograms ("histogram" objects) of same breaks.

weights

a weight for each histogram; if NULL (default), uniform weights are used. Otherwise, it should be a length-\(N\) vector of nonnegative weights.

L

number of quantile levels used to approximate the barycenter (default: 2000). Larger L gives a more accurate approximation at increased computational cost.

Value

a "histogram" object representing the Wasserstein barycenter.

Examples

# \donttest{
#----------------------------------------------------------------------
#                      Binned from Two Gaussians
#
# EXAMPLE : Very Small Example for CRAN; just showing how to use it!
#----------------------------------------------------------------------
# GENERATE FROM TWO GAUSSIANS WITH DIFFERENT MEANS
set.seed(100)
x  = stats::rnorm(1000, mean=-4, sd=0.5)
y  = stats::rnorm(1000, mean=+4, sd=0.5)
bk = seq(from=-10, to=10, length.out=20)

# HISTOGRAMS WITH COMMON BREAKS
histxy = list()
histxy[[1]] = hist(x, breaks=bk, plot=FALSE)
histxy[[2]] = hist(y, breaks=bk, plot=FALSE)

# COMPUTE
hh = histbary(histxy)

# VISUALIZE
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2), pty="s")
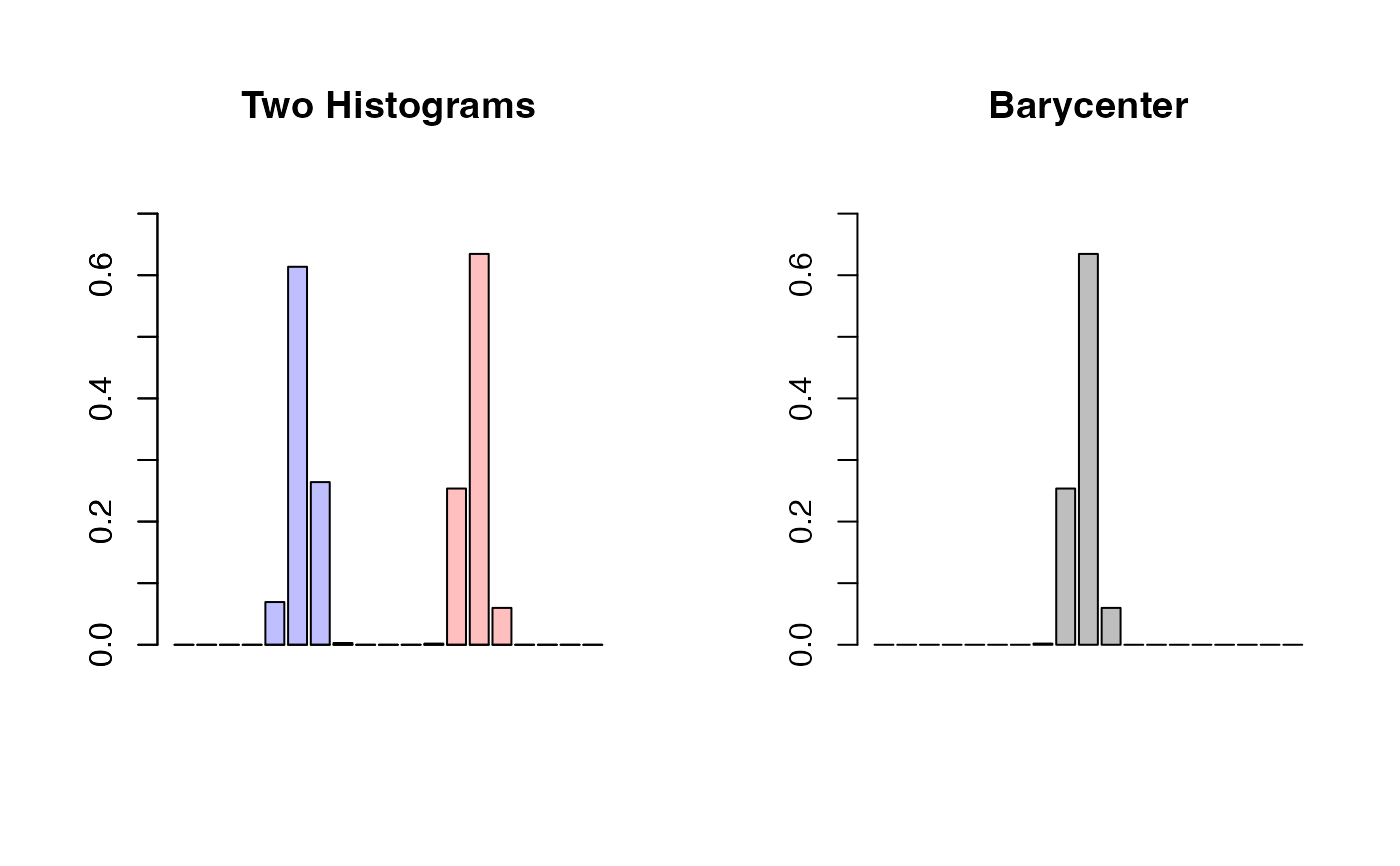
barplot(histxy[[1]]$density, col=rgb(0,0,1,1/4), 
        ylim=c(0, 0.75), main="Two Histograms")
barplot(histxy[[2]]$density, col=rgb(1,0,0,1/4), 
        ylim=c(0, 0.75), add=TRUE)
barplot(hh$density, main="Barycenter",
        ylim=c(0, 0.75))

par(opar)
# }