Distance between Histograms

Compute the \(p\)-Wasserstein distance between two 1D histograms that share the same binning, i.e., same breaks. The histograms are treated as discrete probability measures supported at bin midpoints with masses given by normalized counts. Uses the exact 1D monotone OT algorithm, not LP nor entropic regularization.

Usage

hdist(hist1, hist2, p = 2)

Arguments

hist1

a histogram object (class "histogram").

hist2

a histogram object (class "histogram") with the same breaks as hist1.

p

an exponent for the order of the distance (default: 2).

Value

a named list containing

distance

\(\mathcal{W}_p\) distance value.

Examples

# \donttest{
#----------------------------------------------------------------------
#                      Binned from Gaussian and Uniform
#
# Create two types of histograms with the same binning. One is from 
# the standard normal and the other from uniform distribution in [-5,5].
#----------------------------------------------------------------------
# GENERATE 20 HISTOGRAMS
set.seed(100)
hist20 = list()
bk = seq(from=-10, to=10, length.out=20) # common breaks
for (i in 1:10){
  hist20[[i]] = hist(stats::rnorm(100), breaks=bk, plot=FALSE)
  hist20[[i+10]] = hist(stats::runif(100, min=-5, max=5), breaks=bk, plot=FALSE)
}

# COMPUTE THE PAIRWISE DISTANCE
pdmat = array(0,c(20,20))
for (i in 1:19){
  for (j in (i+1):20){
    pdmat[i,j] = hdist(hist20[[i]], hist20[[j]], p=2)$distance
    pdmat[j,i] = pdmat[i,j]
  }
}

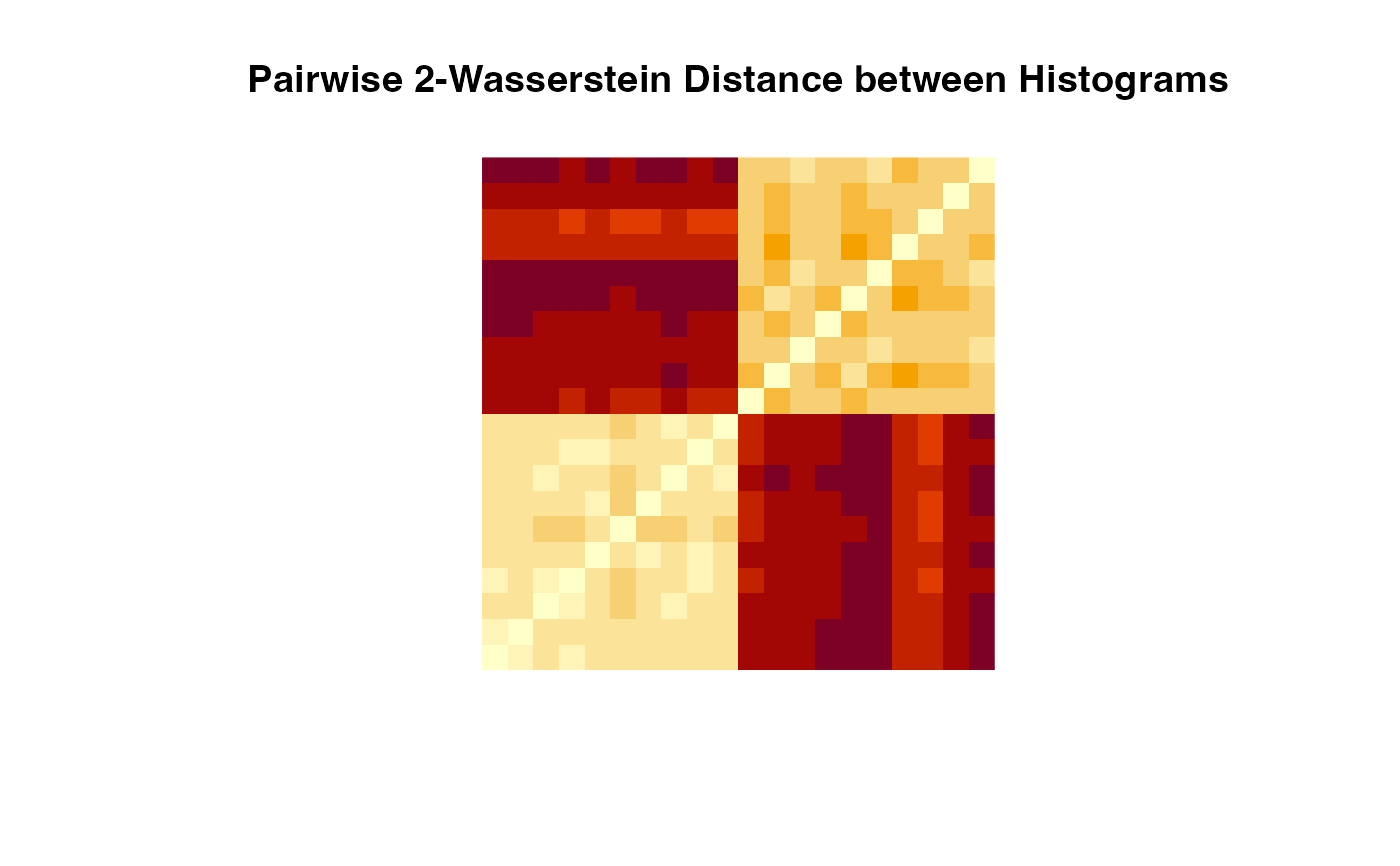
# VISUALIZE
opar <- par(no.readonly=TRUE)
par(pty="s")
image(pdmat, axes=FALSE, main="Pairwise 2-Wasserstein Distance between Histograms")

par(opar)
# }