Wasserstein Median of Empirical CDFs

Given a collection of empirical cumulative distribution functions \(F^i (x)\) for \(i=1,\ldots,N\), compute the Wasserstein median. This is obtained by a functional variant of the Weiszfeld algorithm on a set of quantile functions.

Usage

ecdfmed(ecdfs, weights = NULL, ...)

Arguments

ecdfs

a length-\(N\) list of "ecdf" objects by stats::ecdf().

weights

a weight of each image; if NULL (default), uniform weight is set. Otherwise, it should be a length-\(N\) vector of nonnegative weights.

...

extra parameters including

abstol

stopping criterion for iterations (default: 1e-8).

maxiter

maximum number of iterations (default: 496).

Value

an "ecdf" object of the Wasserstein median.

Examples

# \donttest{
#----------------------------------------------------------------------
#                         Tree Gaussians
#
# Three Gaussian distributions are parametrized as follows.
# Type 1 : (mean, sd) = (-4, 1)
# Type 2 : (mean, sd) = ( 0, 1/5)
# Type 3 : (mean, sd) = (+6, 1/2)
#----------------------------------------------------------------------
# GENERATE ECDFs
ecdf_list = list()
ecdf_list[[1]] = stats::ecdf(stats::rnorm(200, mean=-4, sd=1))
ecdf_list[[2]] = stats::ecdf(stats::rnorm(200, mean=+4, sd=0.2))
ecdf_list[[3]] = stats::ecdf(stats::rnorm(200, mean=+6, sd=0.5))

# COMPUTE THE MEDIAN
emeds = ecdfmed(ecdf_list)

# COMPUTE THE BARYCENTER
emean = ecdfbary(ecdf_list)

# QUANTITIES FOR PLOTTING
x_grid  = seq(from=-8, to=10, length.out=500)
y_type1 = ecdf_list[[1]](x_grid)
y_type2 = ecdf_list[[2]](x_grid)
y_type3 = ecdf_list[[3]](x_grid)

y_bary = emean(x_grid)
y_meds = emeds(x_grid)

# VISUALIZE
opar <- par(no.readonly=TRUE)
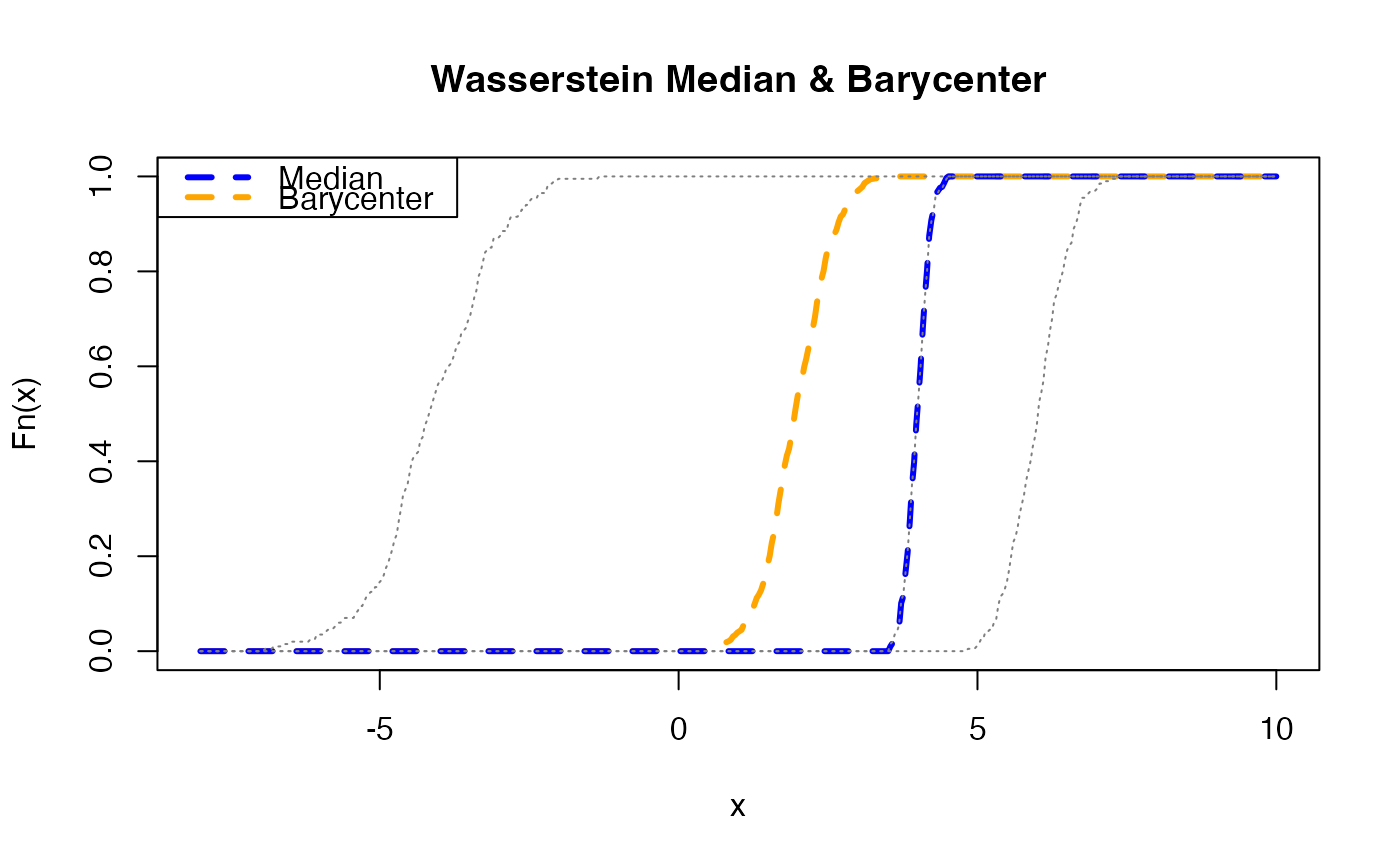
plot(x_grid, y_bary, lwd=3, col="orange", type="l",
     main="Wasserstein Median & Barycenter", 
     xlab="x", ylab="Fn(x)", lty=2)
lines(x_grid, y_meds, lwd=3, col="blue", lty=2)
lines(x_grid, y_type1, col="gray50", lty=3)
lines(x_grid, y_type2, col="gray50", lty=3)
lines(x_grid, y_type3, col="gray50", lty=3)
legend("topleft", legend=c("Median","Barycenter"),
        lwd=3, lty=2, col=c("blue","orange"))

par(opar)
# }