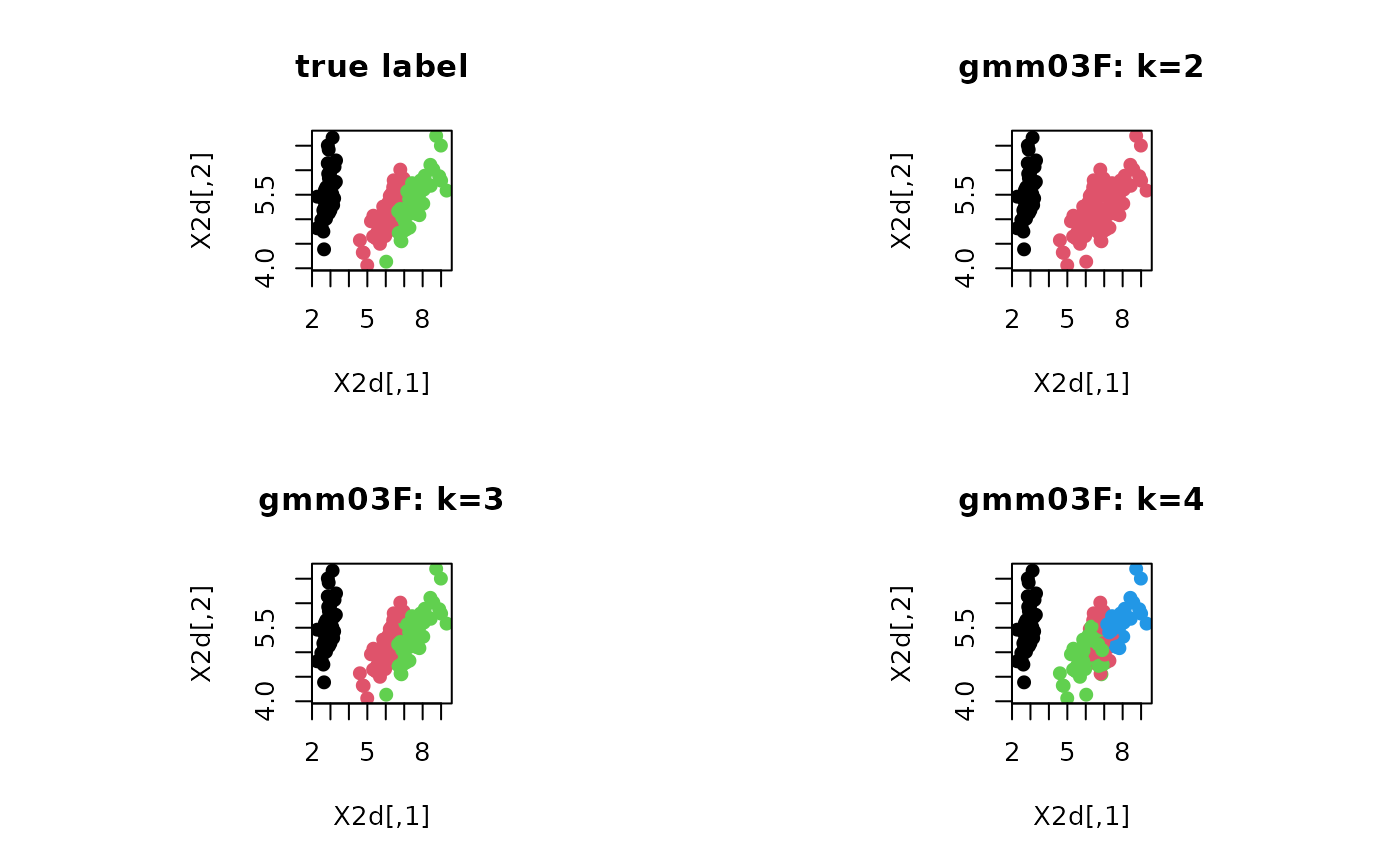Ensemble of Gaussian Mixtures with Random Projection

When the data lies in a high-dimensional Euclidean space, fitting a model-based clustering algorithm is troublesome. This function implements an algorithm from the reference, which uses an aggregate information from an ensemble of Gaussian mixtures in combination with random projection.

gmm03F(data, k = 2, ...)

Arguments

data	an \((n\times p)\) matrix of row-stacked observations.
k	the number of clusters (default: 2).
...	extra parameters including nruns the number of projections (default: 20). lowdim target dimension for random projection (default: 5). maxiter the maximum number of iterations (default: 10). usediag a logical; covariances are diagonal if TRUE, or full covariances are returned for FALSE (default: FALSE).

Value

a named list of S3 class T4cluster containing

cluster

a length-\(n\) vector of class labels (from \(1:k\)).

algorithm

name of the algorithm.

References

Fern XZ, Brodley CE (2003). “Random Projection for High Dimensional Data Clustering: A Cluster Ensemble Approach.” In Proceedings of the Twentieth International Conference on International Conference on Machine Learning, ICML'03, 186–193. ISBN 1577351894.

Examples

# \donttest{
# -------------------------------------------------------------
#            clustering with 'iris' dataset
# -------------------------------------------------------------
## PREPARE
data(iris)
X   = as.matrix(iris[,1:4])
lab = as.integer(as.factor(iris[,5]))

## EMBEDDING WITH PCA
X2d = Rdimtools::do.pca(X, ndim=2)$Y  

## CLUSTERING WITH DIFFERENT K VALUES
cl2 = gmm03F(X, k=2)$cluster
cl3 = gmm03F(X, k=3)$cluster
cl4 = gmm03F(X, k=4)$cluster

## VISUALIZATION
opar <- par(no.readonly=TRUE)
par(mfrow=c(2,2), pty="s")
plot(X2d, col=lab, pch=19, main="true label")
plot(X2d, col=cl2, pch=19, main="gmm03F: k=2")
plot(X2d, col=cl3, pch=19, main="gmm03F: k=3")
plot(X2d, col=cl4, pch=19, main="gmm03F: k=4")
par(opar)
# }