Hierarchical Agglomerative Clustering for Empirical Distributions

Given \(N\) empirical CDFs, perform hierarchical clustering.

ephclust(
  elist,
  method = c("single", "complete", "average", "mcquitty", "ward.D", "ward.D2",
    "centroid", "median"),
  type = c("KS", "Lp", "Wass"),
  p = 2
)

Arguments

elist	a length-\(N\) list of ecdf objects or arrays that can be converted into a numeric vector.
method	agglomeration method to be used. This must be one of "single", "complete", "average", "mcquitty", "ward.D", "ward.D2", "centroid" or "median".
type	(case-insensitive) type of the distance measures (default: "ks").
p	order for the distance for metrics including Wasserstein and lp (default: 2).

Value

an object of hclust object. See hclust for details.

Examples

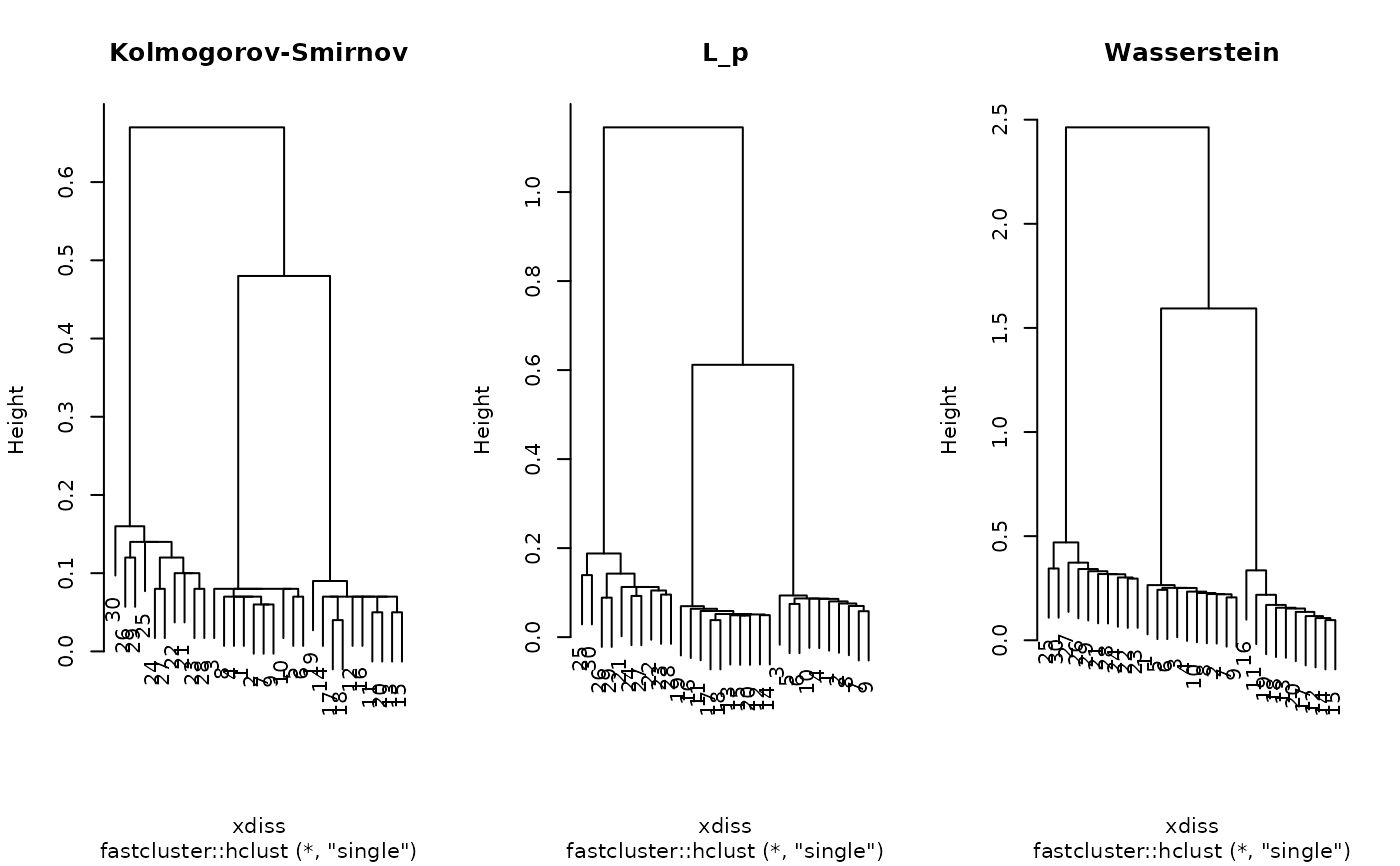
# \donttest{
# -------------------------------------------------------------
#              3 Types of Univariate Distributions
#
#    Type 1 : Mixture of 2 Gaussians
#    Type 2 : Gamma Distribution
#    Type 3 : Mixture of Gaussian and Gamma
# -------------------------------------------------------------
# generate data
myn   = 50
elist = list()
for (i in 1:10){
   elist[[i]] = stats::ecdf(c(rnorm(myn, mean=-2), rnorm(myn, mean=2)))
}
for (i in 11:20){
   elist[[i]] = stats::ecdf(rgamma(2*myn,1))
}
for (i in 21:30){
   elist[[i]] = stats::ecdf(rgamma(myn,1) + rnorm(myn, mean=3))
}

# run 'ephclust' with different distance measures
eh_ks <- ephclust(elist, type="ks")
eh_lp <- ephclust(elist, type="lp")
eh_wd <- ephclust(elist, type="wass")

# visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
plot(eh_ks, main="Kolmogorov-Smirnov")
plot(eh_lp, main="L_p")
plot(eh_wd, main="Wasserstein")
par(opar)
# }