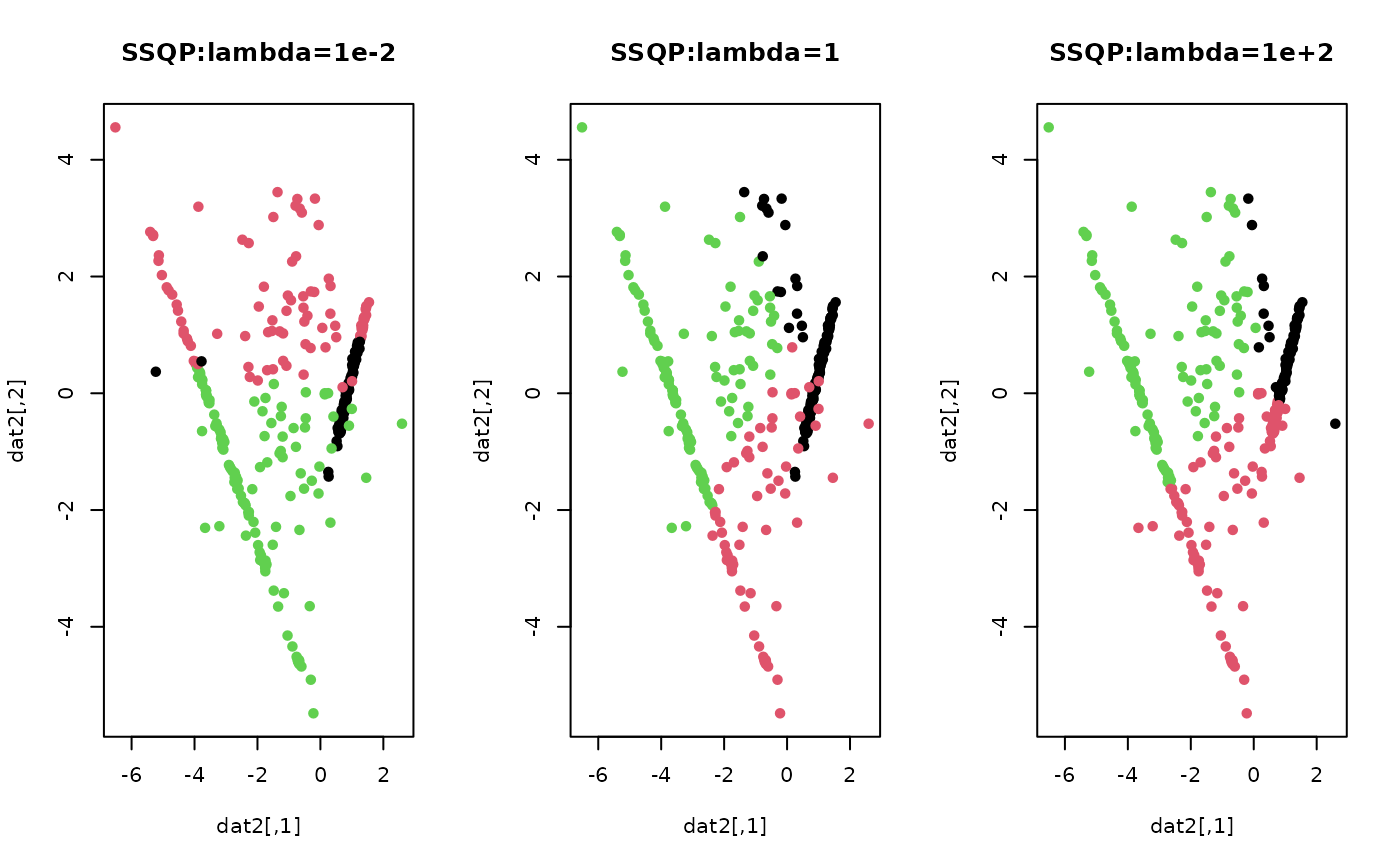Subspace Segmentation via Quadratic Programming

Subspace Segmentation via Quadratic Programming (SSQP) solves the following problem $$\textrm{min}_Z \|X-XZ\|_F^2 + \lambda \|Z^\top Z\|_1 \textrm{ such that }diag(Z)=0,~Z\leq 0$$ where \(X\in\mathbf{R}^{p\times n}\) is a column-stacked data matrix. The computed \(Z^*\) is used as an affinity matrix for spectral clustering.

SSQP(data, k = 2, lambda = 1e-05, ...)

Arguments

data	an \((n\times p)\) matrix of row-stacked observations.
k	the number of clusters (default: 2).
lambda	regularization parameter (default: 1e-5).
...	extra parameters for the gradient descent algorithm including maxiter maximum number of iterations (default: 100). abstol tolerance level to stop (default: 1e-7).

Value

a named list of S3 class T4cluster containing

cluster

a length-\(n\) vector of class labels (from \(1:k\)).

algorithm

name of the algorithm.

References

Wang S, Yuan X, Yao T, Yan S, Shen J (2011). “Efficient Subspace Segmentation via Quadratic Programming.” In Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence, AAAI'11, 519--524.

Examples

# \donttest{
## generate a toy example
set.seed(10)
tester = genLP(n=100, nl=2, np=1, iso.var=0.1)
data   = tester$data
label  = tester$class

## do PCA for data reduction
proj = base::eigen(stats::cov(data))$vectors[,1:2]
dat2 = data%*%proj

## run SSQP for k=3 with different lambda values
out1 = SSQP(data, k=3, lambda=1e-2)
out2 = SSQP(data, k=3, lambda=1)
out3 = SSQP(data, k=3, lambda=1e+2)

## extract label information
lab1 = out1$cluster
lab2 = out2$cluster
lab3 = out3$cluster

## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
plot(dat2, pch=19, cex=0.9, col=lab1, main="SSQP:lambda=1e-2")
plot(dat2, pch=19, cex=0.9, col=lab2, main="SSQP:lambda=1")
plot(dat2, pch=19, cex=0.9, col=lab3, main="SSQP:lambda=1e+2")
par(opar)
# }