Kernel Entropy Component Analysis

Kernel Entropy Component Analysis(KECA) is a kernel method of dimensionality reduction. Unlike Kernel PCA(do.kpca), it utilizes eigenbasis of kernel matrix \(K\) in accordance with indices of largest Renyi quadratic entropy in which entropy for \(j\)-th eigenpair is defined to be \(\sqrt{\lambda_j}e_j^T 1_n\), where \(e_j\) is \(j\)-th eigenvector of an uncentered kernel matrix \(K\).

do.keca(
  X,
  ndim = 2,
  kernel = c("gaussian", 1),
  preprocess = c("null", "center", "scale", "cscale", "whiten", "decorrelate")
)

Arguments

X

an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.

ndim

an integer-valued target dimension.

kernel

a vector containing name of a kernel and corresponding parameters. See also aux.kernelcov for complete description of Kernel Trick.

preprocess

an additional option for preprocessing the data. Default is "null". See also aux.preprocess for more details.

Value

a named list containing

Y

an \((n\times ndim)\) matrix whose rows are embedded observations.

trfinfo

a list containing information for out-of-sample prediction.

entropy

a length-ndim vector of estimated entropy values.

References

Jenssen R (2010). “Kernel Entropy Component Analysis.” IEEE Transactions on Pattern Analysis and Machine Intelligence, 32(5), 847--860.

See also

aux.kernelcov

Author

Kisung You

Examples

# \donttest{
## load iris data
data(iris)
set.seed(100)
subid = sample(1:150,50)
X     = as.matrix(iris[subid,1:4])
label = as.factor(iris[subid,5])

## 1. standard KECA with gaussian kernel
output1 <- do.keca(X,ndim=2)

## 2. gaussian kernel with large bandwidth
output2 <- do.keca(X,ndim=2,kernel=c("gaussian",5))

## 3. use laplacian kernel
output3 <- do.keca(X,ndim=2,kernel=c("laplacian",1))

## Visualize three different projections
opar = par(no.readonly=TRUE)
par(mfrow=c(1,3))
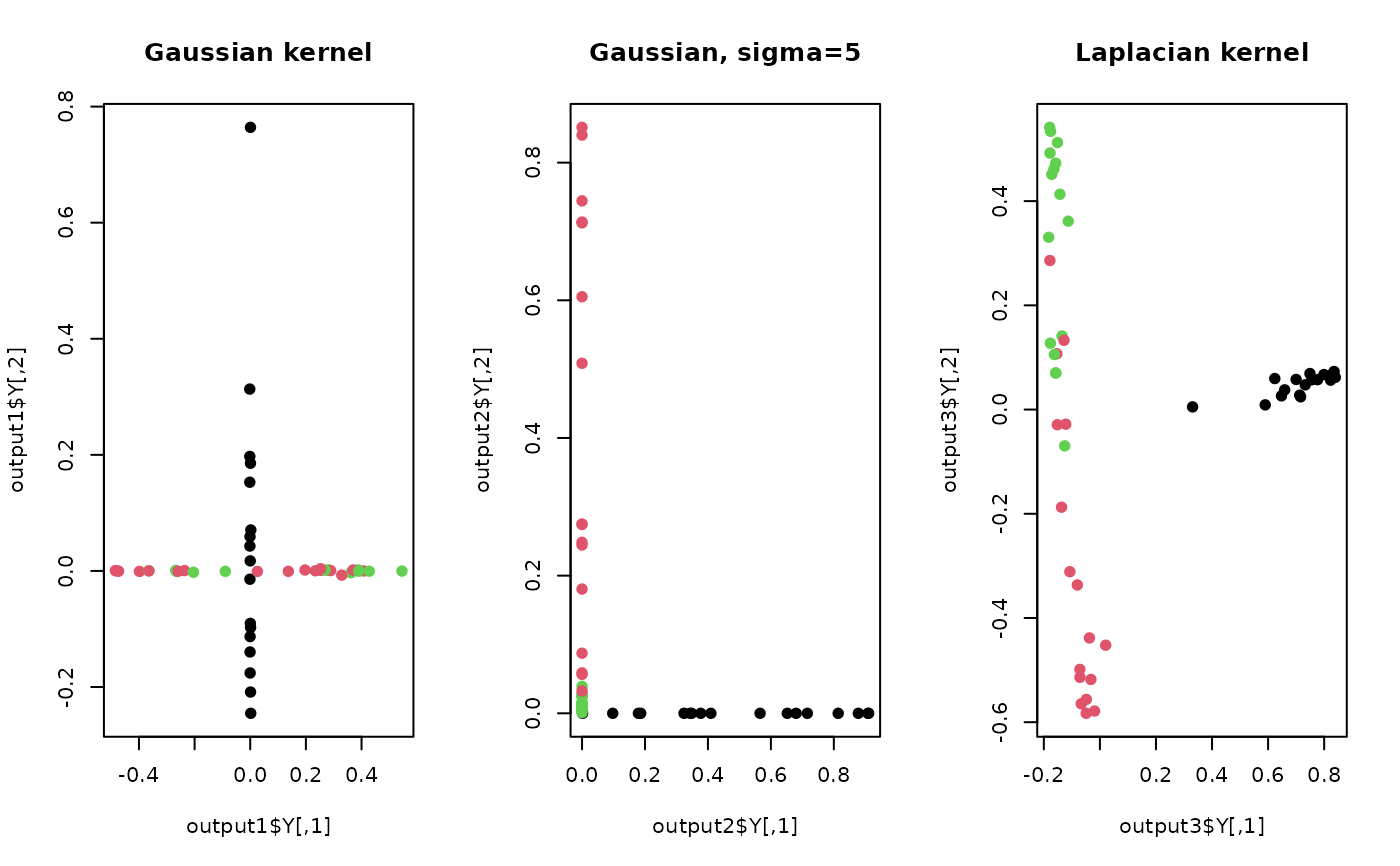
plot(output1$Y, pch=19, col=label, main="Gaussian kernel")
plot(output2$Y, pch=19, col=label, main="Gaussian, sigma=5")
plot(output3$Y, pch=19, col=label, main="Laplacian kernel")

par(opar)
# }