Semi-Supervised Locally Discriminant Projection

Source: R/linear_SSLDP.R

Semi-Supervised Locally Discriminant Projection (SSLDP) is a semi-supervised extension of LDP. It utilizes unlabeled data to overcome the small-sample-size problem under the situation where labeled data have the small number. Using two information, it both constructs the within- and between-class weight matrices incorporating the neighborhood information of the data set.

do.ssldp(
  X,
  label,
  ndim = 2,
  type = c("proportion", 0.1),
  preprocess = c("center", "scale", "cscale", "whiten", "decorrelate"),
  beta = 0.5
)

Arguments

X

an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.

label

a length-\(n\) vector of data class labels.

ndim

an integer-valued target dimension.

type

a vector of neighborhood graph construction. Following types are supported; c("knn",k), c("enn",radius), and c("proportion",ratio). Default is c("proportion",0.1), connecting about 1/10 of nearest data points among all data points. See also aux.graphnbd for more details.

preprocess

an additional option for preprocessing the data. Default is "center". See also aux.preprocess for more details.

beta

balancing parameter for intra- and inter-class information in \([0,1]\).

Value

a named list containing

Y

an \((n\times ndim)\) matrix whose rows are embedded observations.

trfinfo

a list containing information for out-of-sample prediction.

projection

a \((p\times ndim)\) whose columns are basis for projection.

References

Zhang S, Lei Y, Wu Y (2011). “Semi-Supervised Locally Discriminant Projection for Classification and Recognition.” Knowledge-Based Systems, 24(2), 341--346.

Author

Kisung You

Examples

## use iris data
data(iris)
X     = as.matrix(iris[,1:4])
label = as.integer(iris$Species)

## copy a label and let 10% of elements be missing
nlabel = length(label)
nmissing = round(nlabel*0.10)
label_missing = label
label_missing[sample(1:nlabel, nmissing)]=NA

## compute with 3 different levels of 'beta' values
out1 = do.ssldp(X, label_missing, beta=0.1)
out2 = do.ssldp(X, label_missing, beta=0.5)
out3 = do.ssldp(X, label_missing, beta=0.9)

## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
plot(out1$Y, col=label, main="SSLDP::beta=0.1")
plot(out2$Y, col=label, main="SSLDP::beta=0.5")
plot(out3$Y, col=label, main="SSLDP::beta=0.9")

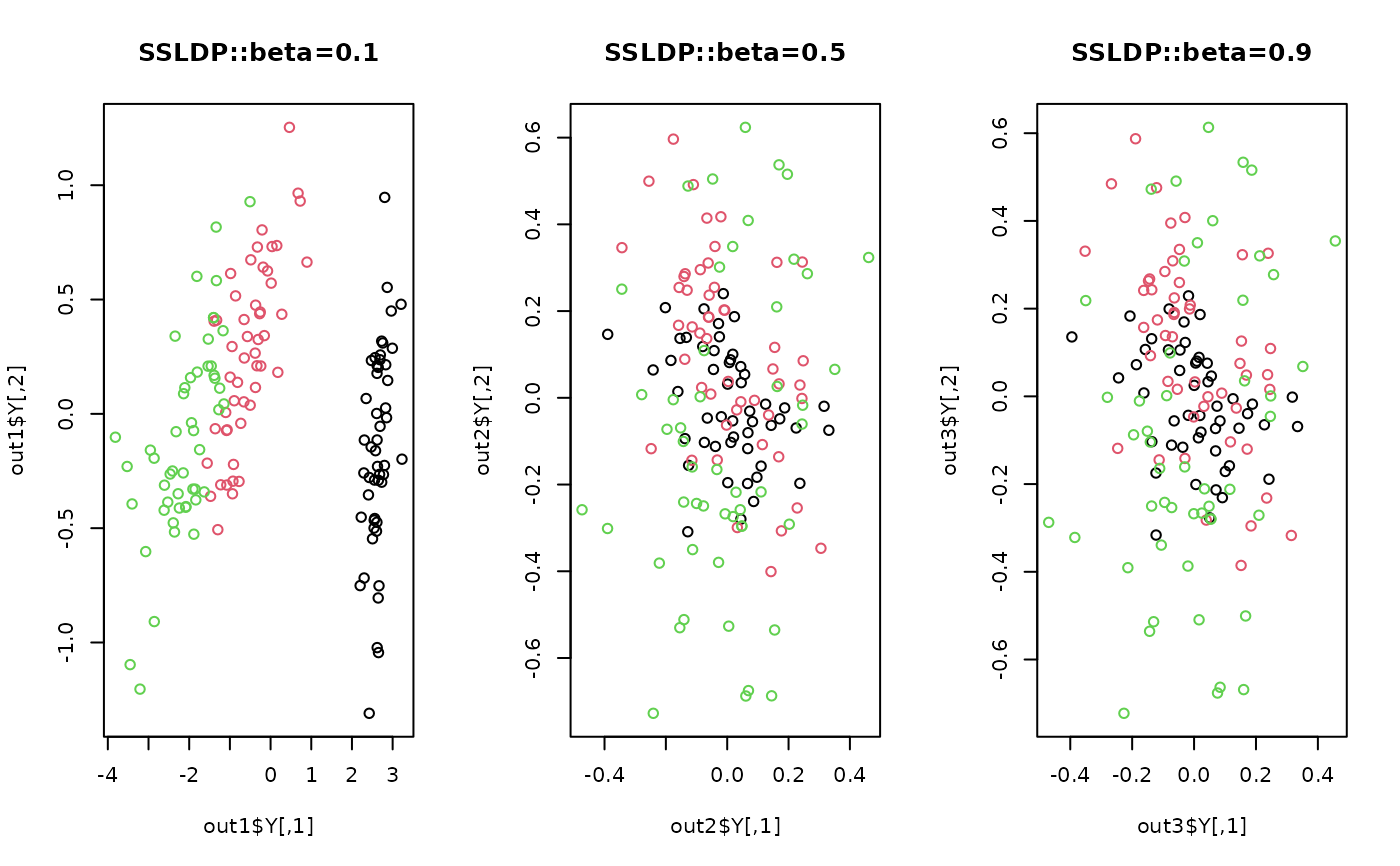par(opar)