Regularized Sliced Inverse Regression

One of possible drawbacks in SIR method is that for high-dimensional data, it might suffer from rank deficiency of scatter/covariance matrix. Instead of naive matrix inversion, several have proposed regularization schemes that reflect several ideas from various incumbent methods.

do.rsir(
  X,
  response,
  ndim = 2,
  h = max(2, round(nrow(X)/5)),
  preprocess = c("center", "scale", "cscale", "decorrelate", "whiten"),
  regmethod = c("Ridge", "Tikhonov", "PCA", "PCARidge", "PCATikhonov"),
  tau = 1,
  numpc = ndim
)

Arguments

X: an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.
response: a length-\(n\) vector of response variable.
ndim: an integer-valued target dimension.
h: the number of slices to divide the range of response vector.
preprocess: an additional option for preprocessing the data. Default is "center". See also aux.preprocess for more details.
regmethod: type of regularization scheme to be used.
tau: regularization parameter for adjusting rank-deficient scatter matrix.
numpc: number of principal components to be used in intermediate dimension reduction scheme.

Value

a named list containing

Y: an \((n\times ndim)\) matrix whose rows are embedded observations.
trfinfo: a list containing information for out-of-sample prediction.
projection: a \((p\times ndim)\) whose columns are basis for projection.

References

Chiaromonte F, Martinelli J (2002). “Dimension Reduction Strategies for Analyzing Global Gene Expression Data with a Response.” Mathematical Biosciences, 176(1), 123--144. ISSN 0025-5564.

Zhong W, Zeng P, Ma P, Liu JS, Zhu Y (2005). “RSIR: Regularized Sliced Inverse Regression for Motif Discovery.” Bioinformatics, 21(22), 4169--4175.

Bernard-Michel C, Gardes L, Girard S (2009). “Gaussian Regularized Sliced Inverse Regression.” Statistics and Computing, 19(1), 85--98.

Bernard-Michel C, Douté S, Fauvel M, Gardes L, Girard S (2009). “Retrieval of Mars Surface Physical Properties from OMEGA Hyperspectral Images Using Regularized Sliced Inverse Regression.” Journal of Geophysical Research, 114(E6).

Author

Kisung You

Examples

## generate swiss roll with auxiliary dimensions
## it follows reference example from LSIR paper.
set.seed(100)
n     = 50
theta = runif(n)
h     = runif(n)
t     = (1+2*theta)*(3*pi/2)
X     = array(0,c(n,10))
X[,1] = t*cos(t)
X[,2] = 21*h
X[,3] = t*sin(t)
X[,4:10] = matrix(runif(7*n), nrow=n)

## corresponding response vector
y = sin(5*pi*theta)+(runif(n)*sqrt(0.1))

## try with different regularization methods
## use default number of slices
out1 = do.rsir(X, y, regmethod="Ridge")
out2 = do.rsir(X, y, regmethod="Tikhonov")
outsir = do.sir(X, y)

## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
plot(out1$Y,   main="RSIR::Ridge")
plot(out2$Y,   main="RSIR::Tikhonov")
plot(outsir$Y, main="standard SIR")

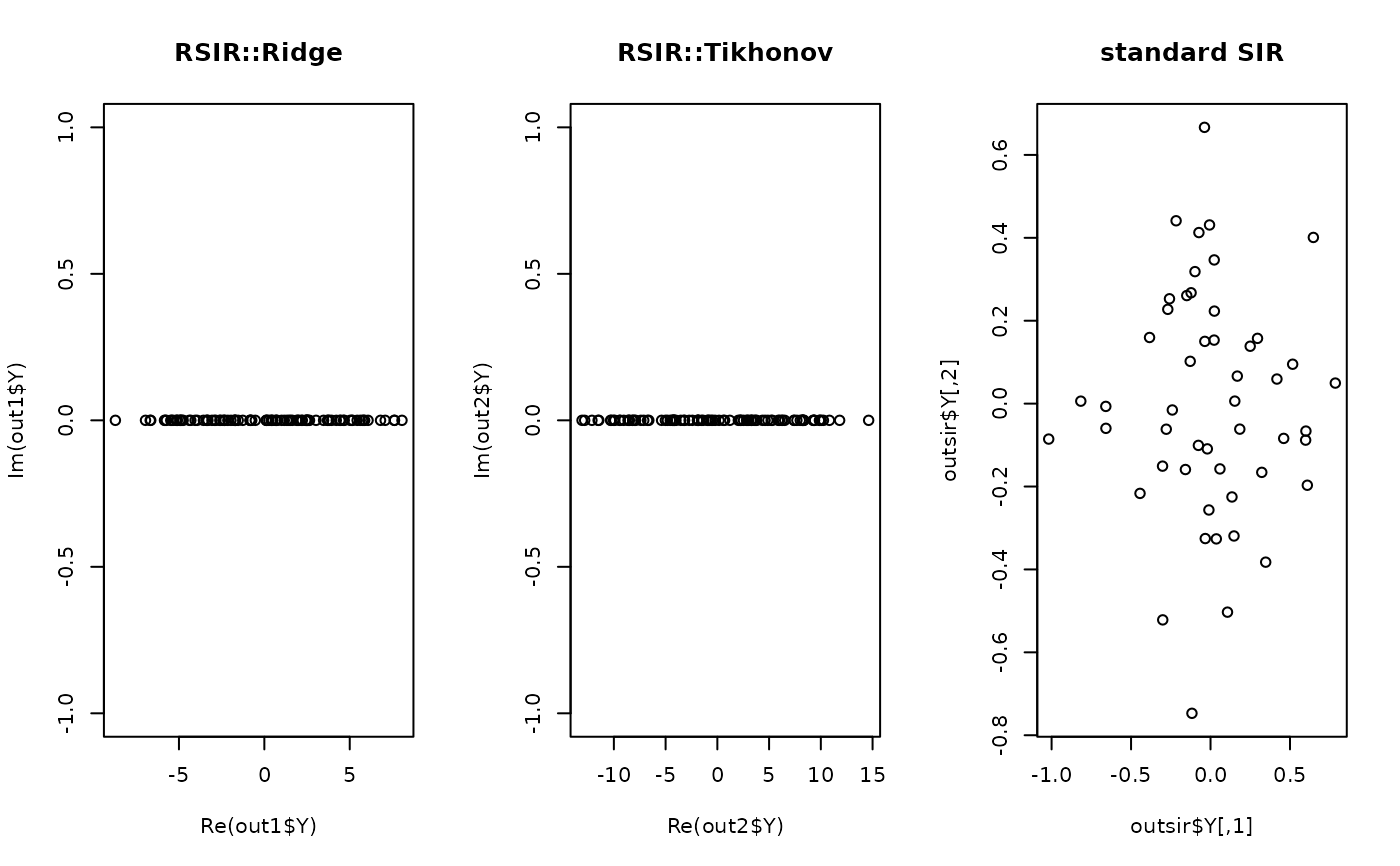par(opar)