Orthogonal Discriminant Projection

Orthogonal Discriminant Projection (ODP) is a linear dimension reduction method with label information, i.e., supervised. The method maximizes weighted difference between local and non-local scatter while local information is also preserved by constructing a neighborhood graph.

do.odp(
  X,
  label,
  ndim = 2,
  preprocess = c("center", "scale", "cscale", "decorrelate", "whiten"),
  type = c("proportion", 0.1),
  symmetric = c("union", "intersect", "asymmetric"),
  alpha = 0.5,
  beta = 10
)

Arguments

X

an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.

label

a length-\(n\) vector of data class labels.

ndim

an integer-valued target dimension.

preprocess

an additional option for preprocessing the data. Default is "center". See also aux.preprocess for more details.

type

a vector of neighborhood graph construction. Following types are supported; c("knn",k), c("enn",radius), and c("proportion",ratio). Default is c("proportion",0.1), connecting about 1/10 of nearest data points among all data points. See also aux.graphnbd for more details.

symmetric

one of "intersect", "union" or "asymmetric" is supported. Default is "union". See also aux.graphnbd for more details.

alpha

balancing parameter of non-local and local scatter in \([0,1]\).

beta

scaling control parameter for distant pairs of data in \((0,\infty)\).

Value

a named list containing

Y

an \((n\times ndim)\) matrix whose rows are embedded observations.

projection

a \((p\times ndim)\) whose columns are basis for projection.

trfinfo

a list containing information for out-of-sample prediction.

References

Li B, Wang C, Huang D (2009). “Supervised Feature Extraction Based on Orthogonal Discriminant Projection.” Neurocomputing, 73(1-3), 191--196.

Examples

## use iris data
data(iris)
set.seed(100)
subid = sample(1:150, 50)
X     = as.matrix(iris[subid,1:4])
label = as.factor(iris[subid,5])

## try different beta (scaling control) parameter
out1 = do.odp(X, label, beta=1)
out2 = do.odp(X, label, beta=10)
out3 = do.odp(X, label, beta=100)

## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
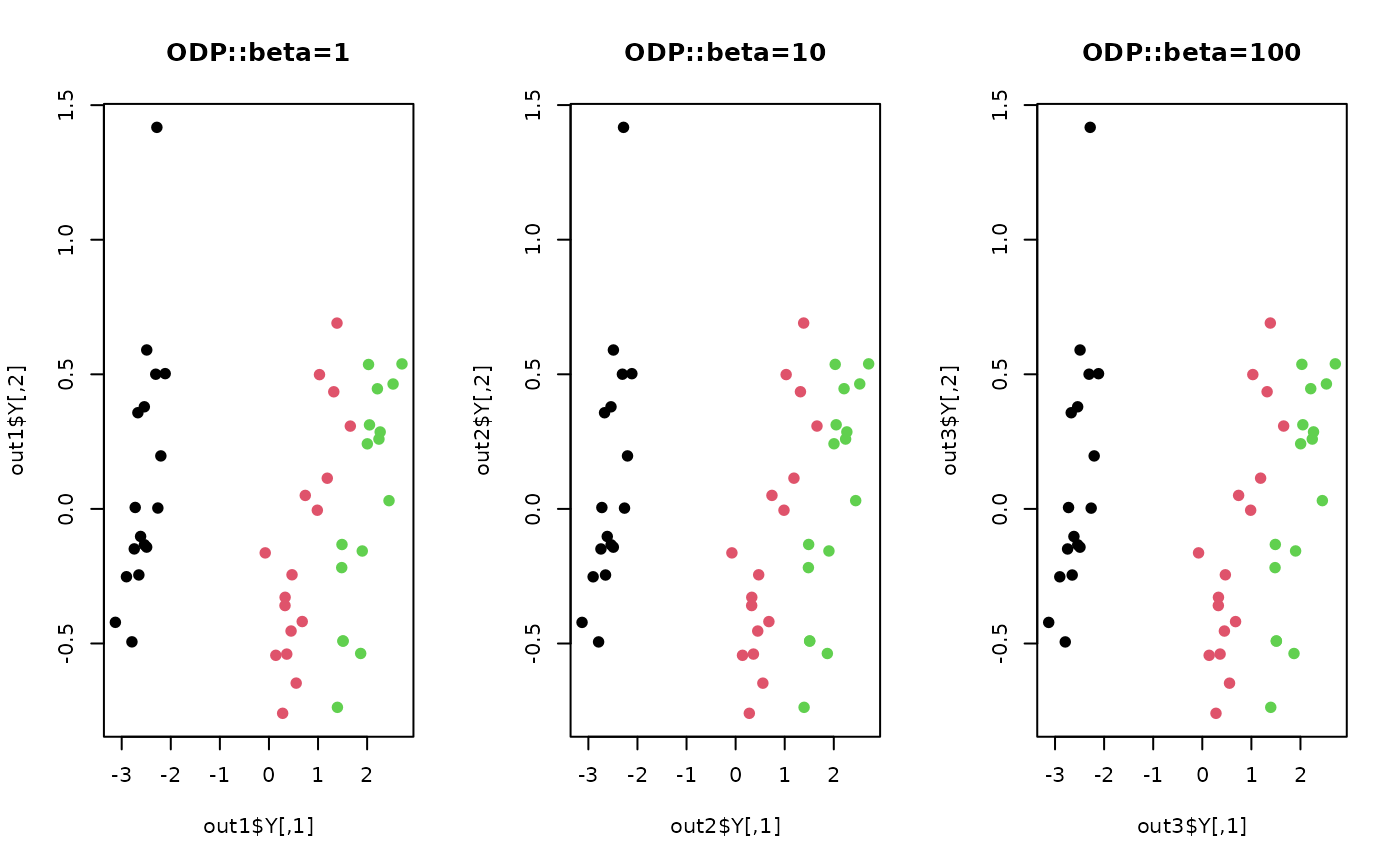
plot(out1$Y, col=label, pch=19, main="ODP::beta=1")
plot(out2$Y, col=label, pch=19, main="ODP::beta=10")
plot(out3$Y, col=label, pch=19, main="ODP::beta=100")

par(opar)